「債券を買ったけど、成績はどうなっているのかな？」と、思われたことはありませんか？
債券投資では投資成果を計るために、「利率」だけでなく「利回り」にも目を向ける必要があります。
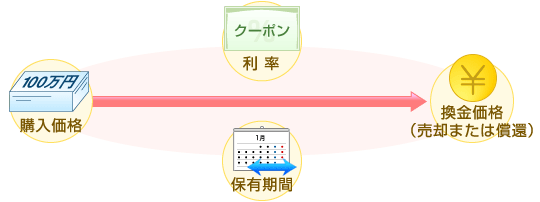
計算のポイントは以下の4つです。
以下の債券を例に計算してみましょう。
米ドル建て外国債券
利率： 年 4.50％（税引前）
残存期間： 4年
購入価格： 額面100米ドルにつき、100米ドル
換金価格（償還価格）：額面100米ドルにつき、100米ドル
計算結果は、4.50％（※）になります。
新たに発行された債券などを償還まで保有すると、購入価格と換金価格（償還価格）が等しくなることが多く、その場合、このように利率（クーポン）と利回りが同じになります。
所有期間：1年6ヶ月（途中売却）
換金価格（売却価格）：額面100米ドルにつき、101米ドル
計算結果は、約5.17％（※）になります。
途中で売却した場合、債券価格の変動により購入価格と換金価格とに差が生じることがほとんどです。この例では、購入価格よりも1米ドル高く売却していますので、利率よりも利回りが高くなっています。
このように、同じ債券でも換金時期によって換金価格が異なり、結果として利回りが異なります。
利回りを計算することで、債券の投資成果を知ることができます。
利回りには、利金や償還金など直接の収入を考慮した「単利」と、受取った利金の再運用益まで考慮した「複利」があります。
上の2つの計算例は単利計算でした。
ここでは、以下の債券を例に、複利計算について簡単に説明します。
米ドル建て外国債券
利率：ゼロクーポン
期間：10年
購入価格：額面1,000米ドルにつき、650米ドル
換金価格：額面1,000米ドルにつき、1,000米ドル
このゼロクーポン債を償還まで保有することを前提に、年1回複利の計算をします。
650米ドルが10年間かかって1,000米ドルになるという債券ですから、年1回複利であれば、以下の計算式が成り立ちます。（650米ドルに利回り（プラス1）の10乗をかけると1,000米ドルになる）
利回りを求めると、約4.40％（※）になります。
年1回複利なので、650米ドルが1年目は約1.044倍になり、2年目はそのまた約1.044倍になり・・・10年目に1,000米ドルになるということになります。
（※）米ドルベースでの利回りとなります。為替変動を考慮した円ベースの利回りとは異なります。
例にあげた2つの債券は、すべて「外貨建て債券」で為替リスクが存在します。
購入時よりも償還時（または売却時）に円安になっていれば、円ベースでは利益が発生することになります。
逆に円高になっていれば、損失が発生します。また、利金についても通常は外貨で支払われますので、同様に為替リスクがあります。
このように、為替変動も投資成果に影響を与えますので、債券そのものの利回りだけでなく、為替リスクにも目を向ける必要があります。
債券投資のポイント
COPYRIGHT © MONEX, Inc.
